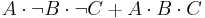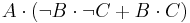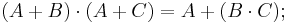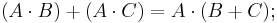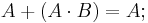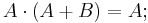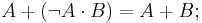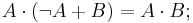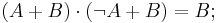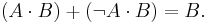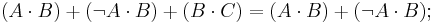Combinational logic

Not to be confused with combinatory logic, a topic in mathematical logic.

In digital circuit theory, combinational logic (sometimes also referred to as combinatorial logic) is a type of digital logic which is implemented by boolean circuits, where the output is a pure function of the present input only. This is in contrast to sequential logic, in which the output depends not only on the present input but also on the history of the input. In other words, sequential logic has memory while combinational logic does not.

Combinational logic is used in computer circuits to do boolean algebra on input signals and on stored data. Practical computer circuits normally contain a mixture of combinational and sequential logic. For example, the part of an arithmetic logic unit, or ALU, that does mathematical calculations is constructed using combinational logic. Other circuits used in computers, such as half adders, full adders, half subtractors, full subtractors, multiplexers, demultiplexers, encoders and decoders are also made by using combinational logic.

Contents

Representation

Combinational logic is used for building circuits where certain outputs are desired, given certain inputs. The construction of combinational logic is generally done using one of two methods: a sum of products, or a product of sums. A sum of products can be easily visualized by looking at a truth table:

A B C Result Logical equivalent
F F F F 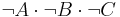\neg A \cdot \neg B \cdot \neg C
F F T F 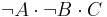\neg A \cdot \neg B \cdot C
F T F F 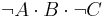\neg A \cdot B \cdot \neg C
F T T F 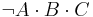\neg A \cdot B \cdot C
T F F T 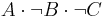A \cdot \neg B \cdot \neg C
T F T F 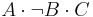A \cdot \neg B \cdot C
T T F F 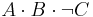A \cdot B \cdot \neg C
T T T T 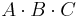A \cdot B \cdot C

Using sum of products, we take the sum of all logical statements which yield true results. Thus, our result would be:

A \cdot \neg B \cdot \neg C %2B A \cdot B \cdot C \,

It could then be simplified using Boolean algebra to:

A \cdot (\neg B \cdot \neg C %2B B \cdot C) \,

Logic formulas minimization

Minimization (simplification) of combinational logic formulas is done using the following rules:

(A %2B B) \cdot (A %2B C) = A %2B (B \cdot C);
\quad (A \cdot B) %2B (A \cdot C) = A \cdot (B %2B C);
A %2B (A \cdot B) = A;
\quad A \cdot (A %2B B) = A;
A %2B (\lnot A \cdot B) = A %2B B;
\quad A \cdot(\lnot A %2B B) = A \cdot B;
(A %2B B)\cdot(\lnot A %2B B)=B;
\quad (A \cdot B) %2B (\lnot A \cdot B)=B.
(A \cdot B) %2B (\lnot A \cdot B) %2B (B \cdot C) = (A \cdot B) %2B (\lnot A \cdot B);

With the use of minimization, a simplified logical function or circuit may be arrived at, and the logic combinational circuit becomes smaller, and easier to analyse, use, or build.

See also

References

External links